Neural Networks for Linear Regressions using Python
Recently, I have been working on a project for Dataverz, the company of my ex-thesis supervisor (and regular collaborator) Pedro Parraguez. I was looking at ways of predicting the number of collaborations between COVID-19 researchers. Here's a small technique I learned during that work.
The data
The data set we built is a (very) large table where every row corresponds to a collaboration between two researchers. In that row, we have information about researcher #1 and researcher #2.
If you are curious about the data, you can learn more about it in this section of my research notebook.
Preparing the problem
The number of collaborations between two researchers is obviously an integer (i.e John and Thomas have 1 co-authored paper on COVID-19). To model this problem we decided to start with a Linear Regression model.
If you are not completely familiar with it, a Linear Regression model looks at all of the columns in your data set, and multiplies each column by a number, with the goal of predicting the column you are interested in, while trying to minimize the error.
Linear Regression Model
My first attempt was to use an off-the-shelf Linear Regression model. One of the most common ones to use, is the scikit implementation. It goes something like this:
# after creating your training and test set..
lr = linear_model.LinearRegression().fit(X_train, y_train)
y_pred = lr.predict(X_test)
This resulted in some OK results. A popular metric to measure how good a Linear Regression model is, is a little something called MAE, you can think about it as an average error per prediction.
After fitting this model, our MAE is sitting at 0.4. This might seem OK at first because it's not a large number. However, most authors only collaborate once (.i.e most rows have a y value of 1), which means that for all of those cases, such an MAE, we are often erring on the number of collaboration by 50%(!).
Here's a graph of some sample collaborations (in black), and some predictions (in red).
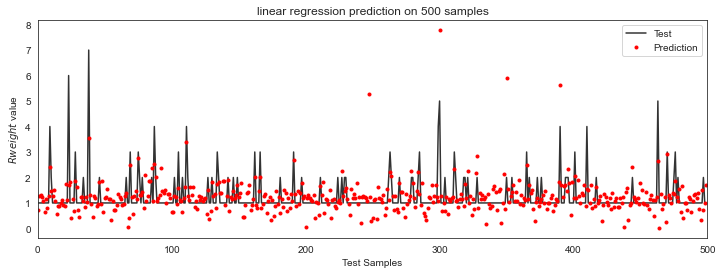
Yeah, that doesn't look great. Notice how the red dots are often very far away from the black line (our truth).
Using a Neural Network
I ended up browsing scikit's documentation for some more time, looking for other viable options to this problem. The documentation is great, really, they even have a page you can use to select an algorithm.
While browsing the Neural Networks page of the docs, I came across what is called, a MLPRegressor.
The MLP Regressor, is basically a Neural Network, that uses squared error as a loss function, and outputs continuous values.
So I gave it a shot:
mlp = pipeline.make_pipeline(preprocessing.StandardScaler(),
neural_network.MLPRegressor(hidden_layer_sizes=(100, 100),
tol=1e-2, max_iter=500, random_state=0)).fit(X_train, y_train)
y_pred = mlp.predict(X_test)
Again, full code here.
This model resulted on an MAE of 0.20, we just reduced our error by 50% (from an MAE of 0.4 to one of 0.2). Here's a graph of some predictions from our neural network regression:
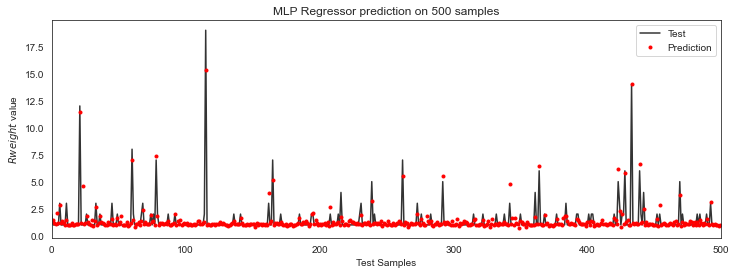
Yeah, that clearly looks much better than the previous one!
This means that for every prediction we are making, we are failing on average about 0.2, which is better taking into consideration that most authors only collaborate once!
Final thoughts
When using Machine Learning to make predictions, starting with the basic models is always the way to go. However, the field is constantly evolving, and it's a good approach to always test out some less traditional techniques, they might surprise you! They for sure surprise me.
Of course, all approaches should still be validated, to make sure they make sense, and that you're not just shooting in the dark.
Here are some links if you want to dig deeper into this work:
- Full article: "Matchmaking experiments using ML and Graph embedding"
- Analysis and code: Jupyter Notebook
- Consulting services